Teoria cinetico-molecolare della temperatura
Relazione tra temperatura assoluta ed energia cinetica media
Relazione di Joule-Clausius - Microreversibilità - Stazionarietà - Isotropia - Statistica e determinismo - Valenza della teoria
La teoria cinetico-molecolare fornisce una spiegazione del concetto di temperatura.
Mediante la relazione di Joule–Clausius, applicata al caso di un gas perfetto, si ricava che la temperatura assoluta di un gas è proporzionale all’energia cinetica media delle particelle, ossia alla loro velocità quadratica media, il cui valore è molto prossimo alla velocità più probabile delle singole particelle.
 Nell'igloo di Fred trovi anche
Nell'igloo di Fred trovi anche
Temperatura ed energia cinetica media delle particelle
In tale relazione una grandezza macroscopica, la
temperatura, è posta in relazione con un valore medio relativo alle caratteristiche cinematiche del moto
delle singole molecole, e quindi tipico della dimensione microscopica della materia.
Poiché la velocità più probabile gode della proprietà di stazionarietà (se non intervengono fattori esterni a perturbare il sistema o scambi termici), anche la
temperatura di un gas risulta costante nel tempo.
Il postulare che gli urti tra le particelle siano elastici porta ad escludere fenomeni di tipo dissipativo a livello microscopico e quindi implica la conservazione dell’energia cinetica: tale idea è supportata dalla nostra esperienza quotidiana ove percepiamo il persistere nel tempo della temperatura di un gas in equilibrio, in pieno accordo con la relazione che lega temperatura ed energia cinetica media delle particelle.
 Nell'igloo di Fred trovi anche
Nell'igloo di Fred trovi anche
APP per convertire le unità di misura
Microreversibilità, stazionarietà e isotropia
In tal senso la microreversibilità dei processi che interessano le particelle risulta fondamentale per assicurare la stazionarietà macroscopica del sistema e
delle sue proprietà.
La casualità e la caoticità del moto delle particelle unite a detta caratteristica di microreversibilità conferiscono al sistema, inoltre, proprietà
di isotropia rispetto alla grandezza fisica temperatura.
Relazione tra macroscopico e microscopico
Così, aumentare la temperatura di un gas significa incrementare l’energia cinetica media delle particelle e fare in modo che esse assumano una maggiore libertà
di movimento: la temperatura svolge, insomma, un’azione “disgregatrice” in contrasto con le deboli forze di coesione tra le varie molecole che caratterizzano
un gas (anche nel caso in cui esso non sia un gas ideale).
Nell'immagine puoi osservare un gas ove le particelle si muovono in maniera veloce: questo è un gas che si trova ad alta temperatura.
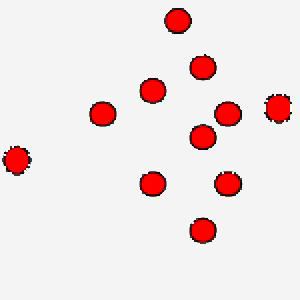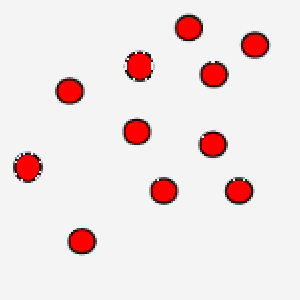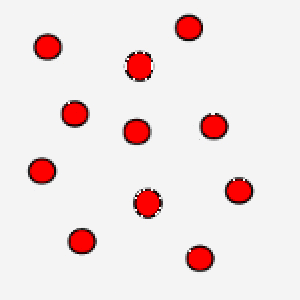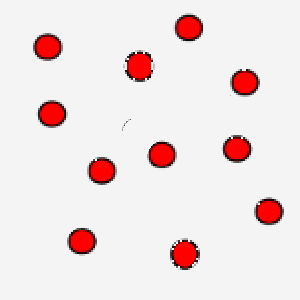
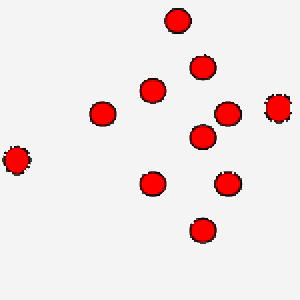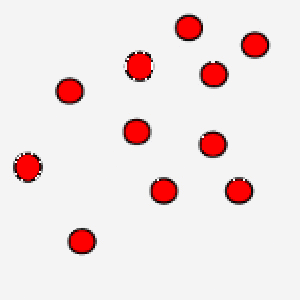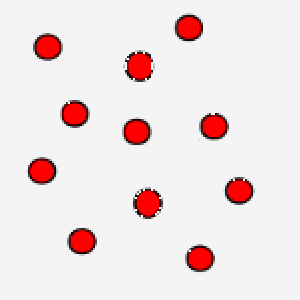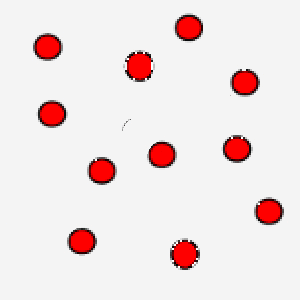
In questa immagine, invece, le particelle hanno un movimento rallentato: questo è tipico di un gas che si trova a bassa temperatura.
La correlazione tra temperatura assoluta ed energia cinetica media assume un’ulteriore valenza se pensiamo che grazie al concetto di velocità media si bypassa la difficoltà di calcolare le equazioni del moto per ogni singola particella, in modo tale, però, da legare comunque una grandezza macroscopica ad un parametro microscopico tipico delle particelle.
Statistica e determinismo
Traspare qui, in maniera evidente, la portata epistemologica di tale concezione: il metodo statistico permette di trattare una caratteristica
di un certo sistema focalizzando l’attenzione su alcune sue caratteristiche microscopiche, pur non implicando la necessità di scendere nella descrizione di
fenomeni che riguardano l’infinitamente piccolo. Il determinismo non permette ciò!
Si può ulteriormente sottolineare come la relazione tra temperatura assoluta del gas ed energia cinetica media non può essere trasposta “tout-court” al caso di
ogni singola molecola. Infatti non avrebbe senso parlare di temperatura di una singola molecola, dato che sarebbe praticamente impossibile calcolare l’energia
cinetica di ognuna di esse che, come abbiamo visto, risulta differire in valore da particella a particella.
La valenza della teoria cinetico-molecolare
In sostanza nella teoria cinetico-molecolare, la temperatura è una proprietà intensiva dei sistemi di cui ha senso parlare solo a livello macroscopico, pur essendo correlata a proprietà microscopiche della materia.