- Conduzione termica
- Convezione termica
- Calore sensibile per cambiare la temperatura
-
Calore specifico
(tabella valori) - Calore latente per il passaggio di stato
- Calore latente e temperatura di solidificazione
- Software per progettare
- Temperatura bulbo umido e di rugiada dell'aria
-
Energia, lavoro, calore
(unità di misura) -
Calore specifico
(unità di misura) -
Coefficiente trasmissione termica
(unità di misura) -
Potenza
(unità di misura) -
Pressione
(unità di misura) -
Temperatura
(unità di misura) -
Lunghezze e distanze
(unità di misura) -
Forza e Peso
(unità di misura)
Conduzione attraverso una parete piana multistrato
Flusso di calore e andamento delle temperature
Materiali diversi - Resistenza al flusso di calore - Condizioni al contorno - Isolanti e conduttori termici
Nella realtà la conduzione termica avviene solitamente attraverso pareti formate da più spessori di materiali diversi (conduzione termica attraverso una parete piana multistrato), aventi quindi una conducibilità termica differente.
Conducibilità termica in regime stazionario
Ricordando l'equazione che lega il flusso di calore e la differenza di temperatura:
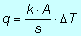
nel caso di parete piana formata da due diversi materiali di conducibilità k1 e k2, detti s1 e s2 lo spessore rispettivamente della prima e della seconda parete, è possibile scrivere in regime stazionario:
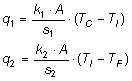
ove TI rappresenta la temperatura della superficie di separazione tra i due materiali.
Ricavando TI dalla prima delle due equazioni e sostituendo nella seconda equazione, ricordando che q1=q2 poiché
non può esservi accumulo di calore sulla superficie di separazione tra i due strati, si ottiene, dopo facili passaggi:
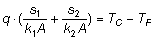
Resistenza termica alla conduzione
Posto s1/k1A=R1 (resistenza termica alla conduzione del materiale 1) e s2/k2A=R2 (resistenza termica alla conduzione del materiale 2) si ottiene:
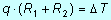
equazione formalmente analoga all'equazione valida per una parete monostrato.
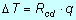
dove la resistenza al flusso di calore è rappresentata questa volta dalla somma delle resistenze offerte da ogni singolo spessore.
Quindi anche nel caso di parete a due spessori permane l'analogia con il caso elettrico.
Parete a più spessori
Il discorso è generalizzabile ad una parete composta da più di due strati di materiale.
Per essa, se n è il numero degli strati, l'equazione ricavata precedentemente si può scrivere:
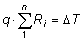
ove Ri rappresenta la resistenza al flusso di calore offerto da ciascun spessore della parete.
Questa è l'equazione che esprime il flusso di calore che si propaga per conduzione attraverso una parete multistrato in funzione della
differenza di temperatura esistente agli estremi della parete.
Andamento delle temperature nella parete multistrato
L'andamento della temperatura all'interno di ogni singolo spessore è decrescente, dalla temperatura "calda" a quella "fredda". Ad esempio, nel caso di parete composta da tre strati, ciascuno di spessore e conducibilità termica differenti, si può rappresentare il grafico della temperatura interna di ciascun strato nel seguente modo:
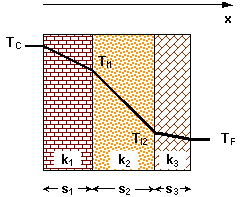
Per ricavare l'espressione analitica dell'andamento della temperatura in ogni spessore occorre integrare opportunamente l'equazione di Fourier:
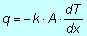
Per il primo spessore di materiale, ricordando che la potenza termica che transita attraverso i vari spessori è sempre la medesima (q1=q2=q3=q) si ha:
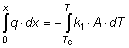
Dopo semplici passaggi matematici è possibile giungere all'espressione:
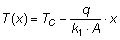
Tale funzione ha come dominio l'insieme delle x comprese tra 0 e s1.
In corrispondenza della superficie di separazione tra il materiale 1 e il materiale 2 (x=s1) si ottiene la condizione al contorno:
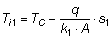
Analogamente per lo spessore 2 è possibile scrivere:
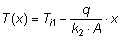
con x compreso tra 0 e s2.
In questo caso in corrispondenza della superficie di separazione tra lo spessore 2 e 3 la condizione al contorno è:
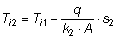
Infine, per lo spessore 3 (x compreso tra 0 e s3)
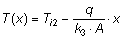
In questo caso la condizione al contorno (x=s3) è:
Cioè la temperatura risulta uguale alla temperatura "fredda", così come deve essere.
Dalle equazioni che esprimono il valore della temperatura T(x) in ogni punto dei vari spessori della parete si evince che la pendenza della retta
è inversamente proporzionale alla conducibilità termica, tipica per ogni strato.
Quindi, per materiali con bassa conducibilità (isolanti) la retta risulta molto inclinata, a conferma dell'alta differenza di temperatura esistente
tra monte e valle lo spessore. Viceversa, per i materiali con buona conducibilità (conduttori), la retta risulta meno inclinata, in quanto tra le due facce
dello spessore la differenza di temperatura è meno pronunciata.
Nell'igloo di Fred trovi anche
